“If you only have a hammer, you tend to see every problem as a nail.” This the law of the instrument, a cognitive bias commonly attributed to the American psychologist Abraham Maslow (1908-1970). The tendency to rely first on what you know is only natural and it is the basis of all learning experiences. You conclude that you’re in a new situation which you’re not ready for only after you’ve tried what you already knew and failed.

When previous experience does give a result, you no longer feel the need to learn. That’s why the law of the instrument is a bias: reliance on it makes you not think or act clearly, because you think you know.

Most of the time, biases appear in social relations, but they could also model our behavior in science. Even our learning of mathematics through abstraction can be biased.

Visual Noise and Optical Illusions

An article published by Science in June 2025 shows an amazing example of how culture dictates the way we see the world, literally. The Himbas, an ethnic group from Namibia (pictured in the featured image), have been studied for years for their multiple particularities. In 2020, BBC wrote about these nomads’ excellent vision, developed while herding the cattle. Since they usually roam in places where there isn’t much vegetation, let alone other visual distractions like roads or buildings, the chromatic diversity of their landscape is mostly monotone. That’s why cattle owners marked their animals using natural dyes of various shades.

Paradoxically, the language of the Himbas does not contain words for shades so diverse (this was shown in another article), as they express verbally mostly primary colors. However, their sight is exceptional, especially in color accuracy, far beyond that of people grown in cities or crowded areas that contain many distractions.

The phenomenon was observed in other rural communities as well, all of which live and develop far from the agitated world and modern civilization. Furthermore, migration influences such abilities. When some native Himbas moved to a modern city, they lost most of their exceptional visual sensibility.

Urban stimuli are numerous, so our brains cannot pay attention to each of them individually. Therefore, brains learned to categorize, sometimes grossly. There’s red and there’s blue, but not many recognize or know burgundy, crimson, teal, or ultramarine, unless they are visual artists or saw or studied such shades explicitly.

But more important than the Himbas’ distinction of color is their reaction to optical illusions. For example, the well-known case of lines of apparently different lengths tricks most of us. We see an abundance of lines in all buildings, furniture pieces, or roads, we also know the illusion of perspective, as well as other geometric relations such as perpendicularity, parallelism, congruence, and more. Hence, due to the overwhelming visual information in our experience, we fail to focus on a simple feature such as length.

The Himbas, however, have no such previous information or experience, hence they are less biased and give a correct answer more frequently. A similar result is obtained by people living in remote rural regions who lived away from all noise and distractions of modern society.

The Science article shows an even finer distinction, in which the life and experience of the Himbas leads to a surprising result. The Coffer Illusion, named after a design on old furniture pieces, hides multiple circles in its apparently rectangular pattern. Most of the people born and raised in modern urban communities need special adjustments or hints to see the circles. Not the Himbas; for them, the situation is reversed: they primarily see the circles and must be instructed specifically to focus on the rectangles.

This phenomenon is explained by their lifestyle and rural organization. They build circular huts (almost hemispherical, like igloos of straws and dirt), because they lead a mostly nomadic life and don’t need durable accommodation. For their cattle, they build circular dens, and around a couple of such huts and dens they erect a fence, thus separating a small village that has a circular border. Hence their bias for circular objects, unlike urban people who are mostly accustomed to rectangular buildings full of lines and angles.

Numbers as Cultural Products

But this isn’t just about the infrastructure and the cognitive biases of the Himba community. The visual perception of circles or rectangles from the coffer illusion has implications on abstract geometric information. The Himba people make the connection between the round shape of their huts and circles in a printed image, hence their propensity towards circular shapes is more general, abstracted from the shapes of objects they are used to. It’s not that they only have eyes trained more on circular objects, but their brains are more used to abstract from those objects to geometric circles.

In 1981, the mathematician and historian Raymond Wilder published the book Mathematics as a Cultural System. The author argues that evolution in general is a cultural phenomenon. Humans, as well as other creatures and the objects they make, including their scientific or abstract theories, evolve in close connection to the culture they belong to. One of the most important cultural elements is language and as John D. Barrow and George Lakoff showed in books that I recommended in a previous article, the vocabulary and the entire linguistic fund of a people influences their evolution, in ways that include their visual perception and how they approach science or mathematics.

If it were only about language, however, mathematics could simply be called a linguistic product, not a cultural one ― but it is much more than that. In a study published in 2008, French neuroscientists Stanislas Dehaene and Véronique Izard showed that cultural elements influence our perception of number lines and ordering.

Usually, the real number line is pictured with numbers in increasing order from left to right. Thus, the abstract “point at infinity” is at its rightmost extrema, and “minus infinity” at its extreme left. But this is also a culturally infused product, as Dehaene and Izard showed. They worked with students from Arab and European countries, who were shown numbers in quick succession, that they had to compare by pressing a button. If the current number is greater than the previous one, a button showing the right direction should be pressed, in the increasing order of numbers on the line.

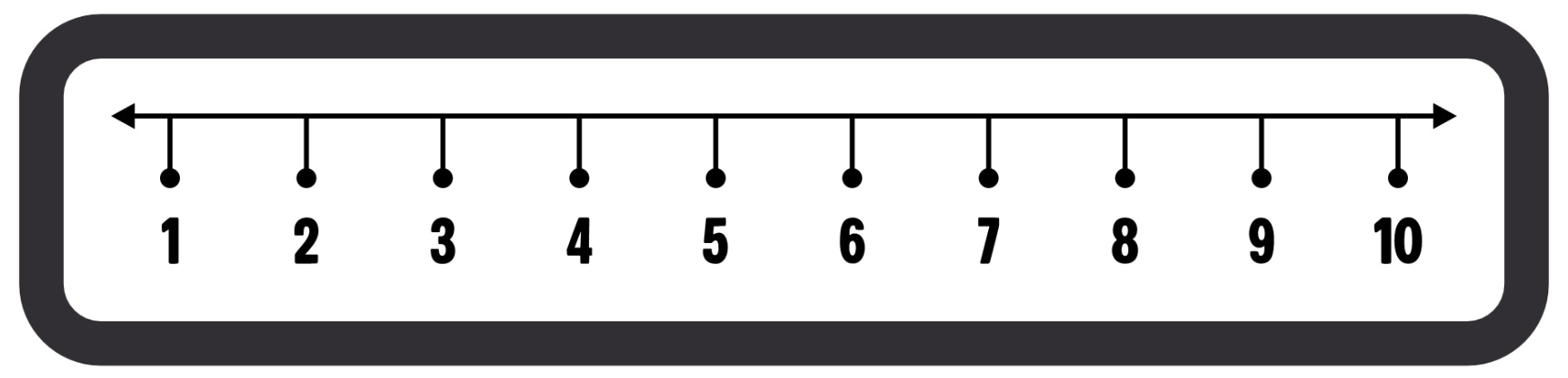
Students born and raised in Arab countries had great difficulties following the rules compared to European students. They often placed larger numbers to the left of smaller ones, corresponding to their right-to-left writing system. Moreover, students who moved to France or other European countries answered more like European natives. The cultural factor, that is the writing system, had a fading influence after approximately ten years. Arab students who had been living for close to a decade in European countries had results that were comparable to European natives.

Nature vs. Nurture in Mathematics

The discussion of mathematical abilities under the influence of cultural backgrounds opens yet another topic, which is wide and old: the nature vs. nurture debate. The examples so far would warrant that nurture is impactful for mathematical abilities such as basic geometry and arithmetic. However, experiments like E. L. Kaufman’s from 1949 or Karen Wynn’s from 1992 showed that there exists a mathematical foundation (at least of arithmetic nature) in each of us. That presumably inborn ability emerges in the first months of our lives, long before any cultural influence could be assimilated.

Kaufman’s study showed that humans have an almost instantaneous ability of “counting” up to six objects. Participants were shown points on a screen for a duration much smaller than the average counting time (less than 300 milliseconds) and were instructed to write their number. When there were at most six points, the accuracy was almost maximum, showing that humans can “count without counting” up to six, an ability that he called subitizing.

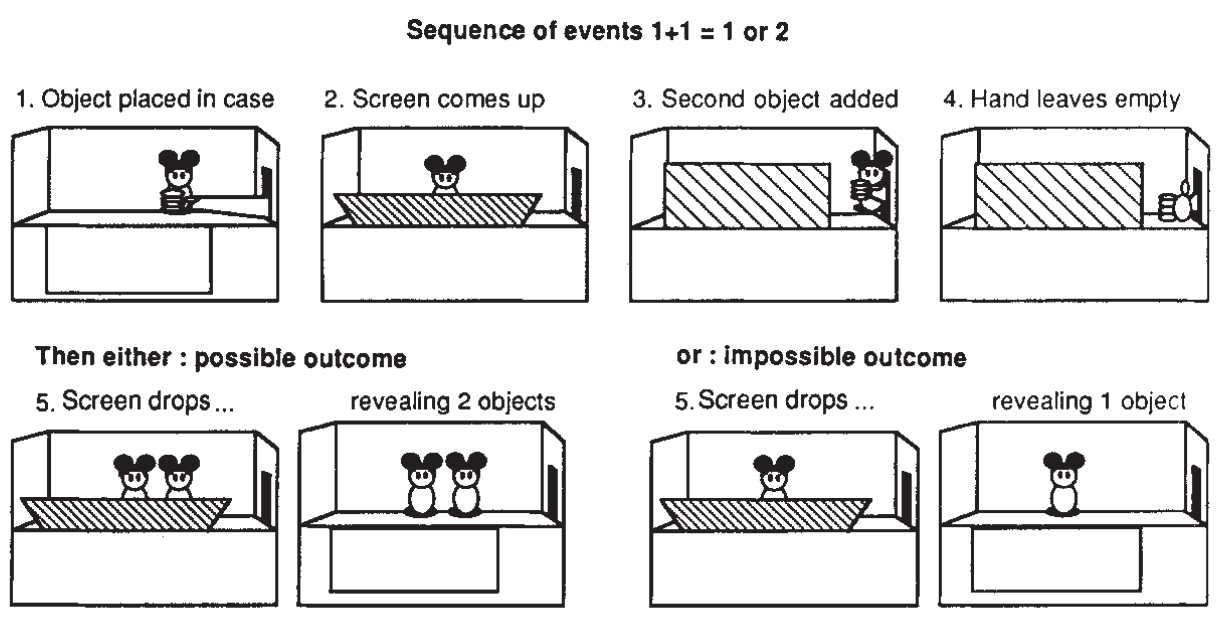
Karen Wynn’s setup was a simple puppet show for infants of at most five months of age. One puppet entered the stage and performed, then the curtain fell. Very visibly, another puppet entered the stage, and when the curtain was raised, infants would see either one or two puppets. The results were clear: when the situation was arithmetically and practically impossible (1 + 1 = 1), infants showed much more curiosity and mimicked not understanding, whereas for the correct situation (1 + 1 = 2), they acted more casually.

Dehaene himself wrote a book, The Number Sense (first published in 1996, second edition in 2011), where he shows that there exists a primitive instinct associated with numbers in the human brain and that it is also present in some animals. He is not the only example: the mathematician Keith Devlin authored a similar book in 2009, titled The Math Instinct: Why You’re a Mathematical Genius (Along with Lobsters, Birds, Cats, and Dogs).

Is Abstraction a Bias?  

Overall, I think the situation is nuanced. The ability to count to six instantaneously or to understand visually and intuitively that 1 + 1 = 2 or distinguishing between circles and rectangles should not be called “mathematics”. However, such elementary tasks are based on an ability to abstract which is essential for any mathematician, regardless of their level. Most education systems start with concrete examples, taken from our everyday lives, which later become more abstract. In fact, most mathematical and scientific knowledge evolved this way: by abstracting concrete situations.

That’s why the capacity of the Himbas to relate the shape of their huts to circles on paper or a screen or some infants’ ability to understand that one puppet means 1 don’t make them mathematicians, but proves they have abstraction abilities, which are essential in mathematics and outside it.

As for the nature vs. nurture debate, there are arguments for inborn elementary abilities, later shaped by culture, education, and evolution. But mathematics and science transcend culture, as brilliant researchers have been emerging all over the world. The access to education is important, and so is belonging to a scientific community, but all of these are built on a foundation whose roots include the ability of abstraction to geometric shapes or numbers and arithmetic from surrounding objects.

Finally, I think that some cognitive biases such as the law of the instrument are not necessarily detrimental for our thinking. Many biases do have negative effects, since the minds of the biased distort reality until it matches the images they formed. But some could also be refined until they become a propensity, closer to a specialization than a faulty link to reality. Thus “the abstract sense”, even when it contains significant cultural nuances, could prove an advantage rather than a defect.